CC Logo

Position Paper: Abstract Networks

Short Form Essay

Another third year essay, this one uses Abstract Networks in order to explain how abstraction, as a concept, is both useful and important to computing.


---



Contents:
-What is a Network?
-What is Abstraction?
-Abstract Network Types:
--Regular
--Small World
--Random
--Scale-Free
-Abstract Networks Within The Real World
-Conclusion
References & Bibliography

What is a Network?

At it's very core, a network is a set of objects that are interconnected through connections (Oxford English Dictionary, 2012). These objects could be anything from people (within a social network) to computing devices like PCs, Laptops or Printers (within a computer network), while the connections between these objects may be anything from social bonds (within a social network) to various cables and radio waves (within a computer network). However, there are many different types of network beyond social or computer based ones, including ones within the human body, such as the Cardiovascular system, which, according to Bupa (2012), is responsible for transferring oxygen-rich blood throughout the human body from the lungs (one type of object) using arteries (the connections) to organs and other places around the body (other objects). Another type of network is a transport network, where destinations (cities, factories and other places) are interconnected by transport links for various vehicles (railways, roads, canals and more).

What is Abstraction?

Abstraction is, according to Stannard, K (2007), the concept of generalizing an object in order to describe only the essential parts that are relevant to a subject without worrying about technical details that may be too complex or other details that may be irrelevant, in order to distinguish it from other objects. Booch, G et al. (2007) note that abstraction is helpful because it allows people to understand information in smaller chunks to build up an understanding of a larger concept.

This can be applied to many fields, such as programming, where Booch, G et al. (2007) describe how each successive generation of programming language after assembly was used to abstract out different parts so that a programmer can create applications to do more useful tasks without dealing with the low-level aspects of assembly where it would not be needed. They note that this abstraction happened in stages, each of them abstracting a different aspect (such as algorithms or data) to make it less complex to use.

Another field where abstraction is used is within art, especially paintings, where famous artists such as Pablo Picasso utilized it. Abstraction within art is, according to Taetzsch, L (2012), a general term covering a variety of techniques that are used to depict something non-concrete (or non-realistic). Hahn, H (2012) notes that in comparison to realistic (or representational) art, the designs within an abstract piece of art may not resemble specific physical objects – in some cases, these may be stylized images of objects, taking only aspects relevant to the artist.

Abstract Network Types

Abstraction can also be applied to aid in understanding the various types of networks – to allow someone to understand them without the technical details. Graham, B (2012) notes that these topological network models can be used as a graphical portrayal that can aid in understanding how a real world network functions. He notes that the objects within these models are called "nodes", while the connections are called "links or edges". He also notes that there are certain measurements that can be derived from these network models: degree (the number of connections to a set note); degree distribution (the distribution of connections within the whole network – how the numbers of connections are distributed is one indicator of the network type; path length (the shortest distance between two set notes, which gives an indication of the connectivity of a network) and clustering (how clustered together the nodes are, this gives some indication of how the network's redundancy).

There are four types of abstract network, each with differing characteristics: Regular; Random; Scale-Free and Small World.

Regular

Graham, B (2012) notes that a regular network is called such because each node has the same number of links and always connects to all of it's nearest neighbours.

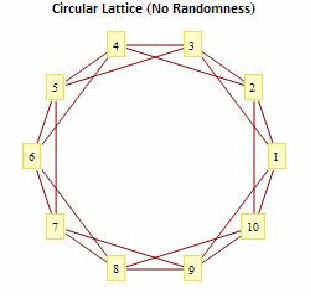
Regular Circular Lattice Network

A regular network with ten nodes and four links from each node to the closest four nodes within the network. Reference: Graham, B (2012)

As can be seen within the diagram, each of the nodes has the same number of connections (what separates a regular network from a random one) and they are all to the closest nodes.

However, it is due to this regularity that one of the main problems of a regular network becomes apparent – where nodes are on opposite ends of the network, there is a high path length between them, which means that the connectivity between these two nodes is low.

Small World

According to Wang, X. F. & Chen, G (2003), Small World networks are named after the “small world effect” - the effect where two previously unconnected objects, often people, discover they both share a connection by way of another object – Smith, D (2008) notes that degrees of separation are used as a measurement between two people (another name for the path length between the two), and reports that a study found that on average, a set of 180 million users of Microsoft Messenger in June 2006 were separated by 6.6 links.

Wang, X. F. & Chen, G (2003) also note Watts and Strongatz proposed that in some cases, this effect can provide for a transition between a regular network and a random one. Newman, M. E. J. (2003) theorises that there may also be a geographical component that causes the effect.

Random

Graham, B (2012) notes that a random network is the opposite to a regular one – rather than each node possessing the same number of links to the closest nodes (a set pattern), the links and the nodes they connect to are entirely random. They are a theoretical construct, originally analyzed by Paul Erdös and Alfred Rényi (in the twentieth century), where each link is chosen randomly with each target node given equal probability.

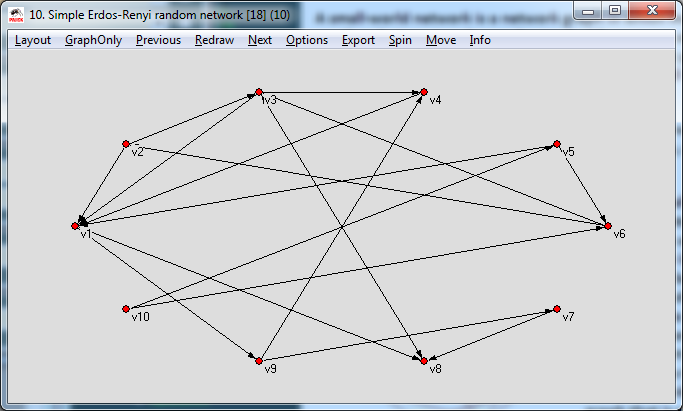
Random Network

A random network with ten nodes and eighteen links created in Pajek.

As can be seen within the diagram, the links do not conform to a set pattern. However, if the number of links is set high enough, eventually every node will become connected to every other node.

Scale-Free

The final type of abstract network is Scale-Free networks. Barabasi, A-L. & Bonabeau, E (2003) state that they were originally derived from an analysis of the World Wide Web by Jeong and Albert (who thought they would find a random network). They differ from both random and regular networks in that while most of the nodes within the network have only a few links, a small proportion will have a large amount (these are called hubs). Graham, B (2012) notes that a commonly seen feature of scale-free networks is a large amount of clustering around the hub nodes.

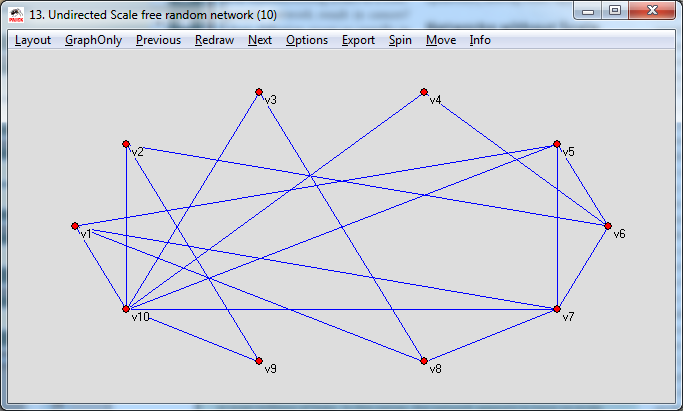
Scale-Free Network

A scale-free network with ten nodes and eighteen links created in Pajek.

This diagram illustrates the nature of a scale-free network to have hubs – within the diagram, nodes v10 and to a lesser extent, v1, v5, v6 and v7 are hubs that provide the interconnection between the nodes that are not hubs. However, because the majority of the links are from only a few nodes, a directed attack at these hub nodes could seriously hamper the connectivity of the network. In addition, because the hub nodes are likely to be connected to one another, this means that the path length between two random nodes is likely to be shorter, as it will go through these hubs.

Abstract Networks Within The Real World

In addition to working as theoretical concepts, abstract networks (especially Scale-Free) can be applied to networks within the real world to aid in understanding – indeed, Scale-Free was originally noticed by researchers who were trying to apply the random network model to the World Wide Web.

Barabasi, A-L. & Bonabeau, E (2003) note that internet could be analysed in two different ways – firstly as a network of web pages (nodes) and the hyper-links (links) connecting them together, and second as the physical network – the devices (nodes) such as servers and client devices and the connections (links), such as fibre optic cable, radio waves like WiFi or Ethernet cables. In both cases, it was discovered that in both cases, the networks fit the Scale-Free model.

Beyond computer based networks, these network models can be seen in areas such as social networks – where Barabasi, A-L. & Bonabeau, E (2003) summarize that social networks often follow a Scale-Free model, whereas Newman, M. E. J. (2003) notes that the small world effect is often seen within social networks (which is fitting, as the name is derived from social situations). Wang, X. F. & Chen, G (2003) note that different transport networks (air or road) may follow different network models – for instance, an air network functions like a scale-free network with several important airports serving as hubs, while a road network may look more like a regular or small-world network, where most places are connected by a similar amount of roads.

Conclusion

In conclusion, Abstraction is an important tool to aid in the understanding of various networks found within nature and the real world, as the abstract networks can provide information that may not be immediately apparent, such as the similarities between the internet and social networks. In addition, this understanding could be expanded upon in order to discover flaws or issues within the networks, such as the internet, as a scale-free network, being open to a targeted attack on hub nodes.



References

Bibliography